Closing the gap: Real OS security finally in reach!

A few years ago we formally verified our seL4 microkernel down to C code. That proof, unprecedented and powerful as it is, didn’t actually establish the security (or safety) of seL4. But the latest achievement of NICTA’s Trustworthy Systems team actually do provide a proof of security.

What the original seL4 verification achieved was a proof that the kernel’s C code correctly implements its specification. The specification is a formal (mathematical) model of the kernel, and the proof showed that the C implementation is “correct”, in the sense that all possible behaviours, according to a semantics of C, are allowed by the spec.

This is both very powerful and limited. It’s powerful in the sense that it completely rules out any programming errors (aka bugs). It’s still limited in three important respects:

1. Ok, the code adheres to the spec, but who say’s the spec is any good? How do you know it’s “right”, i.e. does what you expect it to, is it “secure” in any real sense?
2. The C standard is not a formal specification, and is, in fact, ambiguous in many places. In order to conduct the proof, we had to pick a subset which is unambiguous, and we proved that our kernel implementation stays within that subset. However, we have no guarantee that the compiler, even on our subset, assumes the same semantics!
3. Everyone knows compilers are buggy. So, even if we agree with the compiler about the semantics of our C subset, we can still lose if the compiler produces incorrect code.

Two sets of recent results remove these limitations. One set of work addresses the first limitation, and another the remaining two.

Integrity and confidentiality proofs

What does it mean for the kernel spec to be “good”? It means that the kernel can be used to build the kind of systems we want to build, with the right properties. The specific properties we are after are the classical security properties: Integrity, confidentiality and availability. (For safety a further property is required, timeliness. seL4 has this too, but I’ll discuss this another time.)

Availability is actually a non-issue in seL4: the kernel’s approach to resource management is not to do any, but to leave it to user-level code. The exact model is beyond the level of technicality of this blog, I refer the interested reader to the paper describing the general idea. The upshot is that denial of kernel services is impossible by construction. (This does not mean that availability is necessarily easy to enforce in seL4-based systems, only that you can’t DOS the kernel, or a userland partition segregated by correct use of kernel mechanisms.)

Integrity, at the level of the microkernel, means that the kernel will never allow you to perform a store (write) operation to a piece of memory for which you haven’t been explicitly been given write privilege; including when the kernel acts on behalf of user code. The NICTA team proved this safety property for seL4 about two years ago (see the integrity paper for details). In a nutshell, the proof shows that whenever the kernel operates, it will only write to memory if it has been provided with a write “capability” to the respective memory region, and it will only make a region accessible for writing by user-code (eg by mapping it into an address space) if provided with a write capability.

Confidentiality is the dual to integrity: it’s about read accesses. The figure at the left illustrates this, by showing allowed (black) and forbidden (red) read accesses. However, it turns out that confidentiality is harder to prove than integrity, for two reasons. 1) violation of confidentiality is unobservable in the state of the entity whose confidentiality has been violated 2) confidentiality can be violated not only by explicit reads (loads or instruction fetches) but also by side channels, which leak information by means outside the system’s protection model.

A NICTA team led by researcher Toby Murray has just recently succeeded in proving that seL4 protects confidentiality. They did this by proving what is called “non-interference”. The details are highly technical, but the basic idea is as follows: Assume there is a process A in the system, which holds a secret X. Then they look at any arbitrary execution traces of an arbitrary second process B. If the initial state of the system of any two such traces is identical except for the value of X, they proved that the two traces must be indistinguishable to B. This implies that B cannot infer X, and thus A’s confidentiality is maintained. The technical paper on this work will be presented at next month’s IEEE “Oakland” security conference.

Binary verification

In order to remove from our trusted computing base the C compiler, as well as our assumptions on the exact semantics of C, the team proved that the kernel binary (i.e., the output of the compilation and linking process) is consistent with the formal model of the kernel implementation. This formal model is actually what had earlier been proved to be correct with respect to the kernel spec (it had been obtained by formalising the C code using the formal C semantics). By verifying the binary against the formal model, the formalisation process (and thus our assumptions on the C semantics) are taken out of the trusted computing base.

Binary verification workflow and proof chain

The verification of the binary went in multiple phases, as indicated by the figure on the right. First, the binary was formalised. This was done with the help of a formal model of the ARMv6/v7 architecture. That formalisation of the architecture had previously been done at Cambridge University, in close collaboration with ARM, and is extensively validated. It’s considered to be the best and most dependable formalisation of any main-stream processor.

The formalised binary, which is now a complex expression in mathematical logic inside the theorem prover HOL4, was then “de-compiled” into a more high-level functional form (the left box called “function code” in the figure). This translation is completely done in the theorem prover, and proved correct. Similarly, the formal kernel model is transformed, using a set of “rewrite rules” which perform a similar operation as the compiler does, into a functional form at a similar abstraction level as the output of the above de-compilation. Again, this operation is done in the theorem prover, by application of mathematical logic, and is proved to be correct.

We now have two similar representations of the code, one obtained by de-compilation of the binary, the other by a partial compilation process of the formalised C. What is left is to show their equivalence. Readers with a CS background will now say “but that’s equivalent to the halting problem, and therefore impossible!” In fact, showing the equivalence of two arbitrary programs is impossible. However, we aren’t dealing with two arbitrary programs, but with two different representations of the same program (modulo compiler bugs and semantics mismatch). The operations performed by a compiler are well-understood, and the re-writing attempts to retrace them. As long as the compiler doesn’t change the logic too much (which it might do at high optimisation levels) there is hope we can show the equivalence.

And indeed, it worked. The approach chosen by Tom Sewell, the PhD student who did most of the work, was to compare the two programs chunk-by-chunk. For each chunk he used essentially a brute-force approach, by letting an SMT solver loose on it. Again, some trickery was needed, especially to deal with compiler optimisations of  loops, but in the end, Tom succeeded. Details will be presented at the PLDI conference in June.

The resulting tool is fairly general, in that it is not in any way specific to seL4 code, although it has limitations which are ok for seL4 but might be show-stoppers for other code. Specifically, the tools can’t deal with nested loops (but seL4 doesn’t have any, nor should any microkernel!) At present, the tools grok the complete seL4 binary when compiled by gcc with the -O1 optimisation flag. We normally compile the kernel with -O2, and this introduces a few optimisations which presently defeat the tool, but we’re hopeful this will be fixed too.

This is actually quite a significant result. You may have heard of Ken Thompson’s famous Turing Award Lecture “Reflections on trusting trust“, where he describes how to hack a compiler so it will automatically build a back door into the OS. With this tool, seL4 is no longer susceptible to this hack! If the compiler had built in a back door, the tool would fail to verify the correctness of the binary. But regular compiler bugs would be found as well, of course.

Where are we now?

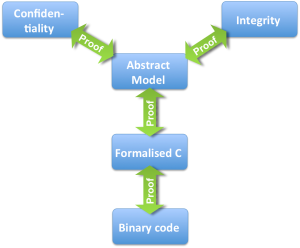We now have: 1) Proofs that our abstract kernel spec provides integrity and confidentiality; 2) A proof that the formalised C code is a correct implementation of the kernel spec; and 3) a proof that the kernel binary is a correct translation of the formalised C code. Together this means that we have a proof that the kernel binary has the right security properties of enforcing confidentiality and integrity!

There are still some limitations, though. For example, we haven’t yet verified the kernel’s initialisation (boot-strap) code, this is work in progress (and is nearing completion). There are also bits of unverified assembler code in the kernel, and we don’t yet model the operation of the MMU in detail. So there are still some corners in which bugs could, in theory, be hiding, but we’re getting closer to sweeping out the last refuges of potential bugs.

A more fundamental issue regards the side channels mentioned above. These are traditionally classified into two categories: storage channels and timing channels. The difference is essentially whether a common notion of time is required to exploit them.

In principle our non-interference proof covers storage channels, up to the point to which hardware state that could constitute a channel is exposed in the hardware model that is used in the proof. Presently that model is fairly high-level, and therefore might hide potential storage channels. It does cover things like general-purpose CPU registers, so we know that the kernel doesn’t forget to scrub those in a context switch, but modern CPUs have more complex state that could potentially create a channel. Nevertheless, the approach can be adapted to an arbitrarily-detailled model of the hardware, which would indeed eliminate all storage channels.

Timing channels are a different matter. The general consensus is that it is impossible to close all timing channels, so people focus on limiting their bandwidth. So far our proofs have no concept of time, and therefore cannot cover timing channels. However, we do have some promising research in that area. I’ll talk about that another time.